Part 1
Kubus - Balok - Prisma - Limas
Bangun ruang adalah sebuah bangun tiga dimensi yang mempunyai volume atau isi ruang serta dibatasi oleh sisi-sisi. Pada pembahasan kali ini, kita hanya akan membahas bangun ruang yang dibatasi oleh sisi yang berbentuk datar.
1. Kubus
Perhatikan gambar berikut:
Kubus adalah bangun ruang yang dibatasi oleh enam sisi yang berbentuk persegi. Bisakah kalian menyebutkan benda di sekitar kalian yang berbentuk kubus?Unsur-unsur dalam kubus diantaranya adalah rusuk,
- Pada kubus tersebut terdapat 12 rusuk.
- Rusuk-rusuk pada kubus memiliki ukuran yang sama panjang.
- Rusuk AB sejejar dengan rusuk CD, EF, dan GH.
- Rusuk BC sejajar dengan rusuk AD, EH, dan FG.
- Rusuk AE sejajar dengan rusuk BF, CG, dan DH.
Luas permukaan Kubus
Luas permukaan kubus dapat dihitung dengan menjumlahkan luas seluruh sisi-sisinya. Karena keenam sisinya berbentuk persegi maka:
Luas I = Luas II = Luas III = Luas IV = Luas V = Luas VI = Luas persegi
Luas persegi = r x r
Luas permukaan kubus = Luas I + Luas II + Luas III + Luas IV + Luas V + Luas VI
Lp = (r x r) + (r x r) + (r x r) + (r x r) + (r x r) +(r x r)
Luas Permukaan Kubus = 6 x r x r = 6r2
Secara ringkas rumus Kubus sebagai berikut:
| Volume kubus | V = s x s x s |
| Luas permukaan kubus | L = 6 x (s x s) |
| Keliling kubus | K = 12 x s |
| Luas salah satu sisi | L = s x s |
2. Balok
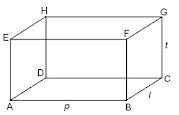
Balok merupakan bangun ruang yang dibatasi oleh tiga pasang sisi sejajar yang berbentuk persegi atau persegi panjang dengan setidaknya terdapat satu pasang sisi sejajar yang memiliki ukuran yang berbeda.Pada sebuah balok berlaku:
- Mempunyai 6 sisi, sisi yang berhadapan memiliki bentuk dan ukuran yang sama.
- Mempunyai 8 titik sudut.
- Mempunyai 12 rusuk.
Secara ringkas rumus Balok sebagai berikut:
| Volume Balok | V = p x l x t |
| Luas permukaan balok | L = 2 x ( pl + lt + pt) |
| Diagonal ruang | d = √( p2+ l2 + t2 ) |
| Keliling balok | K = 4 x (p + l + t) |
3. Prisma
Prisma merupakan salah satu jenis bangun ruang yang dibatasi oleh sisi alas dan sisi tutup serta sisi-sisi tegak yang berbentuk persegi atau persegi panjang.Karakteristik prisma segi-n yaitu sebagai barikut.
- Prisma memiliki n + 2 sisi. 2 sisi yaitu sisi alas dan sisi tutup serta n sisi tegak.
- Banyaknya titik sudut pada prisma adalah 2n.
- Prisma memiliki 3n rusuk, n rusuk pada sisi alas, n rusuk pada sisi tutup, dan n rusuk pada sisi tegak.
| Volume prisma segitiga | V = luas alas x t |
| Luas permukaan prisma segitiga | L = keliling alas x t + 2 x luas alas segitiga |
4. Limas
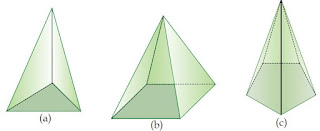
Limas tersusun dari beberapa segibanyak. Secara umum, limas dapat diartikan sebagai salah satu bangun ruang sisi datar yang dibatasi oleh sebuah sisi alas yang berupa segibanyak dan sisi-sisi tegak yang berbentuk segitiga. Salah satu titik sudut dari masing-masing segitiga tersebut bertemu pada satu titik yaitu titik puncak limas.
Pemberian nama pada limas berdasarkan pada bentuk alasnya. Suatu limas yang alasnya berbentuk segitigas disebut dengan limas segitiga, limas dengan sisi alas berbentuk segiempat diberi nama limas segi empat, dan begitu pula dengan sisi alas yang berbentuk segibanyak lainnya.
Limas segiempat
Volume limasV = 1/3 x p x l x t
Luas permukaan limasL = luas alas + luas selubung limas
Limas segitiga
Volume limas segitigaV = 1/3 x luas alas x t
Luas permukaanL = Luas alas + Luas selubung limas
Diolah dari berbagai sumber Buku dan Internet